Perché i PC usano il codice binario?
Il binario è un sistema di numeri di base 2. Base 2 significa che ci sono solo due cifre: 1 e 0 che corrispondono agli stati acceso e spento e che quindi il tuo computer può capire. Probabilmente hai familiarità con la base 10, il sistema decimale. Il sistema decimale utilizza dieci cifre che vanno da 0 a 9, quindi si avvolge per formare numeri a due cifre, con ogni cifra che vale dieci volte di più dell’ultima (1, 10, 100, ecc.). Il binario è sostanzialmente simile, con ogni cifra che vale due volte di più dell’ultima.
Conteggio in binario
In binario, la prima cifra vale 1 in decimale. La seconda cifra vale 2, la terza vale 4, la quarta vale 8, e così raddoppia ogni volta. Facciamo un piccolo esempio:
1010 = dieci
scomponendo le cifre numeriche partendo da destra abbiamo:
0^0: 0 1^1: 2 0^3: 0 1^4: 8
Quattro bit binari ci danno 16 cifre, se passiamo a 8 bit otterrai 256 valori possibili. Ciò richiede molto più spazio per rappresentare i numeri poiché quattro cifre in decimale ci danno 10.000 valori possibili. I computer comprendono il binario molto meglio di quanto noi comprendiamo i decimali. Certo, il binario occupa più spazio, ma siamo trattenuti dall’hardware. E per alcune cose, come l’elaborazione logica, il binario è migliore del decimale.
C’è un altro sistema di base che viene anche usato nella programmazione: esadecimale. Sebbene i computer non siano esadecimali, i programmatori lo usano per rappresentare gli indirizzi binari in un formato leggibile dall’uomo durante la scrittura del codice. Questo perché due cifre esadecimali possono rappresentare un intero byte: otto cifre in binario. Esadecimale usa 0-9 come il decimale, ed utilizza inoltre anche le lettere da A ad F per rappresentare le sei cifre aggiuntive.
Quindi, perché i computer usano il binario?
La risposta breve: l’hardware e le leggi della fisica. Ogni numero nel tuo computer è un segnale elettrico, e nei primi giorni dell’informatica, i segnali elettrici erano molto più difficili da misurare e controllare molto precisamente. Aveva più senso distinguere solo tra uno stato “on” rappresentato da una carica negativa e uno stato “off”, rappresentato da una carica positiva. Per chi non è sicuro del perché “spento” è rappresentato da una carica positiva, è perché gli elettroni hanno una carica negativa: più elettroni significano più corrente con una carica negativa.
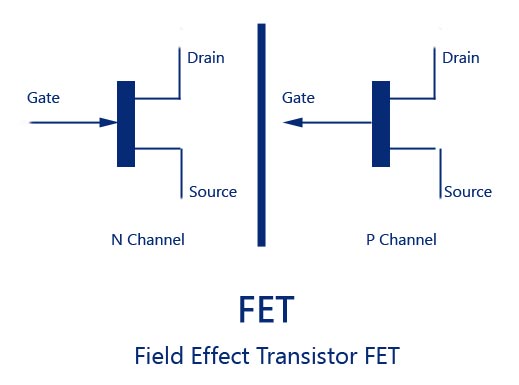
Quindi, i primi computer di dimensioni normali utilizzavano il codice binario per costruire i loro sistemi, e anche se usavano hardware molto più vecchio e ingombrante, abbiamo mantenuto gli stessi principi fondamentali. I computer moderni usano ciò che è noto come transistor per eseguire calcoli con codice binario. Ecco un’immagine di come si presenta un transistor ad effetto di campo (FET):
Essenzialmente, consente solo alla corrente di fluire dalla sorgente allo scarico se c’è una corrente nell’uscita. Questo forma un interruttore binario. I produttori possono costruire questi transistor incredibilmente piccoli, fino a 5 nanometri, o circa le dimensioni di due filamenti di DNA. Questo è il modo in cui operano le moderne CPU, e anche loro possono soffrire di problemi che distinguono tra stati acceso e spento (anche se ciò è dovuto principalmente alla loro dimensione molecolare irreale, essendo soggetti alla stranezza della meccanica quantistica).
Ma perché solo Base 2?
Quindi potresti pensare “perché solo 0 e 1? Non potresti semplicemente aggiungere un’altra cifra? “Mentre alcuni di essi si riferiscono alla tradizione, e cioè nel modo in cui i computer sono stati costruiti, aggiungere un’altra cifra significherebbe che dovremmo distinguere tra diversi livelli di corrente, non solo “spento” ed “acceso”, ma anche “un po’” e “molto”.
Il problema qui è che se si desidera utilizzare più livelli di voltaggio, è necessario un modo per eseguire facilmente calcoli e con l’hardware non è fattibile come sostituzione per il calcolo binario. In effetti esiste; si chiama computer ternario, ed è in circolazione dagli anni ’50, ma questo è praticamente il punto su cui si è fermato lo sviluppo. La logica ternaria è molto più efficiente di quella binaria, ma fino ad ora, nessuno ha un sostituto efficace per il transistor binario, o per lo meno non è stato fatto alcun lavoro per svilupparli alle stesse minuscole scale del binario.
Il motivo per cui non possiamo usare la logica ternaria si riduce al modo in cui i transistor sono impilati in un computer – qualcosa chiamato “gate” – e in che modo vengono utilizzati per eseguire la matematica. I gate accettano due input, eseguono un’operazione su di essi e restituiscono un’uscita.
Questo ci porta alla lunga risposta: la matematica binaria è molto più semplice per un computer di qualsiasi altra cosa. La logica booleana si associa facilmente ai sistemi binari, con True e False rappresentati da acceso e spento. I gate del computer operano sulla logica booleana: prendono due input ed eseguono un’operazione su di essi come AND, OR, XOR e così via. Due ingressi sono facili da gestire.
Chissà? In futuro, potremmo iniziare a vedere i computer ternari diventare una cosa, poiché spingiamo i limiti del binario a un livello molecolare. Per ora, però, il mondo continuerà a funzionare su file binari.





Social